ECE 4590/6590 Integrated Circuit Design (23 Fall)
Undergraduate/Graduate course lab session, Clemson University, Holcombe Department of Electrical and Computer Engineering, 2023
Design concepts and factors influencing the choice of technology; fundamental MOS device design; silicon foundries, custom and semicustom integrated circuits; computer-aided design software/hardware trends and future developments; hands-on use of CAD tools to design standard library cells; systems design considerations, testing, and packaging.
Lab materials
This semester, we’ve transitioned from the previous HSpice-based lab offerings using the Synopsys toolchain to a new setup employing the Cadence toolchain and SPECTRE. The overall lab setting replicates similar lab settings in prior semesters with minor difference in Lab 0, Lab 1, Lab 2, Lab 3. Apart from that, I modified and introduced Lab 4, Lab 5 and changed the final project topic, and enhanced the experience with a more hands-on approach to CMOS integrated circuit design. Apart from that, part of the RTL2GDSII workflow was introduced in the lab session. The content provided has been revised post the 2023 Fall course offering and may not undergo further updates in the foreseeable future. To make the lab run smoothly, you must load your SPECTRE, VIRTUOSO, and library properly. We use 45nm standard voltage temperature CMOS model throughout the lab,.
The lab content below was adapted from Cadence training tutorials available within Cadence site. You may click the link below to jump to the corresponding labs. It is recommended to adhere to the identical format outlined in the provided script example for each individual lab, as minor differences may lead to unexpected errors.
Lab 1 SPECTRE & DC analysis of NMOS and PMOS
Lab 2 SPECTRE transient analysis and measurement
Lab 4 Delay of combinational logic
Lab 5 Combinational Logic Family, Wire, Sequential Logic
Lab 6 Final project 2-bit full adder
Lab Extra RTL 2 GDSII workflow
Lab 0 Familar with the tool
Learning objective
This lab is expected to familarize with the Cadence tools.
Lab procedures
Load request a node with X11 forwarding capability using your prefered ssh tool. You need to load the required cadence tool Virtuoso (IC/618) and SPECTRE (SPECTRE/211). Most of the cadence’s tool documents are located within its installation path.
Run the simulation script, you need to run the command under the identical directory of provided SPECTRE circuit script for lab 0.
spectre inv.scs +log inv.log
- Type the command below to allow the wavefrom viewer pop out and you can later load the waveform stored in .raw file generated by the SPECTRE. Note, there is a space between a and & below.
viva &
Using the provided SPECTRE circuit script for lab 0, you need to identify the location of your Cadence library for gpdk45, at the begining of the script, which is
include "YOUR_GPDK_LIBRARY.scs" section=ttserved as a placeholder.Within the Viva wavefrom viewer after load the generated .raw file, you are expected to see three waveform stored in .raw file:
- An input-output voltage relation of an inverter with input voltage range from 0 to 1.1V, using dc analysis.
- An input-output voltage relation of an inverter with input voltage range from 1.1V/2 to 1.1V, using dc analysis.
- An input-output voltage relation of an inverter with input voltage as an pulse wave using transicent analysis.
These three types of waveforms are the ones used throughout the lab assignements.
Generated file types
Along the following lab, multiple files will be generated, below are the ones will happen this lab:
- .log file for the running process output.
- .raw file for the waveform and all data.
- .measure file for all detialed measurements.
- .mt file for table-like measurement results.
Explaination of the circuit script
The script describes the description of a simple inverter, whether implemented with or without a subcircuit. The connections can be referenced as follows:
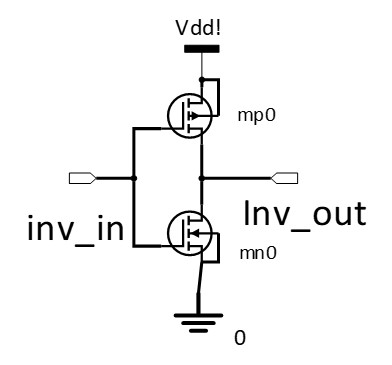
The one shown below is the one using subcircuit.
subckt invs_subckt inv_out inv_in mp1 (inv_out inv_in vdd! vdd!) g45p1svt w=w_p l=l_p mn1 (inv_out inv_in 0 0) g45n1svt w=w_n l=l_n ends invs_subckt
g45n1svt, g45p1svt represent the type of NMOS/PMOS transistor used in this circuit, and w, l represent the width and length of the circuit. Within the SPECTRE, the transistors ports are ordered as (drain gate source body). mp1, mn1 are the name of the transistor. Within this subcircuit, the node vdd!, and 0 define the power supply and ground, and vdd itself is the power supply voltage.
dc_analy0 dc param=vs0 start=0 stop=vdd step=0.01 shows the instantiation of the direct-current source named as dc_analy0, with voltage start from 0 to vdd with step size of 0.01V, while v1 (inv_in2 0) vsource dc=vs2 type=pulse val0=0 val1=vdd period=10u rise=5p fall=5p width=5u defines another pulse wave fed to inv_in2 port. trans1 tran stop=10u method =trap should go along with this pulse wave input to allow the correct transicent anlayis, with trap stands for the trapezoidal method for internal numerical anlaysis. ‘simOptions options temp=25’ define the temperature used for the simulation.
The provided SPECTRE circuit script for lab 0 has been intentionally designed with high parameterization, enabling easy modifications to align with specific lab requirements. This flexibility allows for straightforward adjustments to suit varying needs and specifications.
Lab 1 SPECTRE & DC graphic analysis of NMOS and PMOS
This lab is expected to learn how to do detial DC analysis using NMOS and PMOS. The students are provided with SPECTRE circuit script for lab 1 as example. Based on the provided example, students are expected to explore the various parameters of 45nm gpdk library.
Save transistor parameters
save xx.yy:zz allows you to save the zz parameter of the xx.yy device. For the library used here, the naming follows bsim4 simulation model. xx. can be omitted if the target transistor does not belong to a subcircuit.
- Ids: Resistive drain-to-source current
- ueff: Effective mobility at the specified analysis temperature
- all: Everything
- vdsat: Drain-source saturation voltage
- vgs: Gate-source voltage
- vth: Threshold voltage
Library width, length, temperature limitation
The transistor models within the library adhere to restrictions based on width and length, ensuring optimal simulation accuracy. You can find detailed information in the documentation located under the installation path of the library.
Sweep analysis
Sweep analysis provides the flexibility to modify one parameter or variable, such as $V_{gs}$,with a set of limited values, while maintaining higher precision for other parameter(s) like $V_{ds}$. It operates as a “for loop” in its representation:
For (vgs) from vgs1 to vgs5: Record xx for dc analysis.
The syntax used in SPECTRE is shown as following, which is also avaliable in SPECTRE circuit script for lab 1.
swp_a sweep param=vgs start=0 stop=? step=? {
dc_a dc param=vds start=0 stop=? step=?
}
Lab assignements
Below are the ones we do for this semester, students are highly encouraged to solidate all measurement within one script file, and leverage the parameterized design to ease the difficulties to complete this assignment.
- Graph on $ I_{ds} $ versus $ V_{gs} $ (for different $ V_{ds} $ ) for both NMOS and PMOS.
- Graph on $ I_{ds} $ versus $ V_{ds} $ (for different $ V_{gs} $ ) for both NMOS and PMOS.
- Sub-threshold swing for both NMOS and PMOS.
- Body Effect for both NMOS and PMOS.
- DIBL (Drain-induced barrier lowering) ($ V_{ds} $ versus $ V_{th} $) for both NMOS and PMOS.
- DIBL (Drain-included barrier lowering) (Length versus $ V_{th} $) for both NMOS and PMOS
- Graph on Temperature versus $ V_{th} $ for both NMOS and PMOS
Lab 2 SPECTRE & DC numerical analysis of NMOS and PMOS
Lab objectives
This lab focuses on extracting and computing various parameters and values using the graphic waveform and MDL tools to complete the measurement. Students are provided with SPECTRE circuit script for lab 2 and MDL script for lab 2.
Apart from that, the concept of Monte Carlo simulation was also introduced. , while not included as lab assignment. This part directly used the MDL_workshop tutorial under the SPECTRE installtion path.
Performing measurement for channel length modulation coefficient
Channel length modulation is one of the effects of short-channel Field Effect Transistors (FET). It can be included in $I_{ds}$ computation as follows if the FET is in velocity saturation:
\(I_{ds}=\beta(V_{gs}-V_t-V_{dsat}/2)V_{dsat}(1+\lambda V_{ds})\).
$\lambda$ is the channel length modulation coefficient. If we consolidate $\beta(V_{gs}-V_t-V_{dsat}/2)V_{dsat}=k$, then we can easily find $I_{ds}=k(1+\lambda V_{ds})$, and then calculated by finding the slop and one data point. The slope can be derived by Viva. Similar computation can be done in the rest of the lab assignment.
Measurement Description Language (MDL)
MDL is a scripting and measurement language that enhances productivity during simulation and analysis.
Advantages:
- It create alias measurements that can be reused in different circuits, allowing efficiently run simulations in batch mode.
- Parameterize alias measurements, making them reusable over various applications.
- Use the wildcard (*) in the MDL control file for all signal mapping.
- No need to have GUI if you only care about the value.
MDL example
Within the provided MDL script for lab 2, a simple measurement is done.
alias measurement dc {
run dc_sweep_nmos
export real mn0_vdsat_0p0=mn0:vdsat@0
}
run dc
Define the measurement name: alias measurement dc Run the dc analysis by run dc_sweep_nmos which is the name you give to the dc sweep analysis, NOT the .scs file. Export the value of mn0:vdsat when sweep value is 0. The result will be printed in .measure file .
There exist two types of commands to run the MDL script, as shown below:
spectremdl -batch lab02.mdl -design lab02.scs +log lab02.log spectre +mdl lab02.mdl -design lab02.scs +log lab02.log
Monte Carlo Analysis
The reason we introduce Monte Carlo here is to give students the impression that even we define the gates with identical width, and length, they still can be different in actual manufaction. Process variance contributes the difference, and possibly hurts circuit performance.
- Purpose of Monte Carlo:
- Investigate how device mismatches in a circuit can affect the circuit as a whole.
- Done based on statistical distributions and calculate each parameter randomly according to a statistical distribution model.
- The result is a range of possible outcome values.
- Calculate the probabilities of different outcomes and perform additional analyses.
From the guest lecture for Cornell ECE 5545, Cerebras by Sean Lie available at https://www.youtube.com/watch?v=5_qVob2Vwf8, it discussed how the real-world large chip design needs to consider such a variance.
Within the MDL, it allows different statistic block to specify the statistic variation patterns. The statistics blocks allow you to specify batch-to-batch (process) and per-instance (mismatch) variations for netlist parameters. These statistically-varying netlist parameters can be referenced by models or instances in the main netlist and may represent IC manufacturing process variation or component variations for board-level designs.
Lab assignements
Based on the provided SPECTRE circuit script for lab 2 and MDL script for lab 2, students are expected to find and compute explore the various parameters of 45nm gpdk library. Below are the ones we do for this semester.
- Use the $ I_{ds} $ Versus $ V_{ds} $ graph (for fixed $ V_{gs} $) to calculate the channel length modulation coefficient ($\lambda$) (NMOS), when $ V_{gs}=V_{dd}, V_{ds}=[0,V_{dd}] $
- Calculate velocity saturation ($ c_{ox}\cdot v_{sat} $ ) (NMOS), when $ V_{gs}=V_{dd}, V_{ds}\in [0,V_{dd}] $
- Print a set of Saturation Voltage ($V_{DSat}$) (NMOS) when $ V_{gs}=[0,0.02,V_{dd}], V_{ds}=V_{dd}, V_{bs}=0$
- Show the results in ‘.measure’ file.
- Manually plot the set of $V_{DSat}$ dots on the Ids versus $V_{ds}$ plot for different $ V_{gs}$
- Find the Sub-threshold slope factor (NMOS) when $V_{gs}=[0,V_{dd}], V_{ds}=V_{dd}, v_{bs}=0$
- Examine the body effect ($k_\gamma$) (NMOS) when $V_{gs}=V_{dd}, V_{ds}=V_{dd}, v_{bs}=[-V_{dd},V_{dd}]$
- Find NMOS and PMOS mobility ratio ($\mu_n/\mu_p$))
- Calculate Critical Voltage: $V_c=E_c\cdot L$(NMOS) when $V_{gs}=V_{dd}; V_{ds}=V_{dd}, v_{bs}=0$.
- The computation needs to use the Equation: $V_{DSat}=\frac{((V_{gs}-V_{th})\cdot E_c\cdot L)}{((V_{gs}-V_{th})+E_c\cdot L)}$
- Calculate $I_{DSat}$ (NMOS):
- $V_{gs}=V_{dd}, V_{ds}=V_{dd}, v_{bs}=0, t_{ox}=3nm$
- Use Equation: $I_{DSat}=\frac{W}{L}\cdot \frac{µ_{eff}\cdot C_{ox}\cdot E_{c}\cdot L}{2} \frac{(V_{gs}-V_{th})^2}{((V_{gs}-V_{th})+E_c\cdot L)}$
- Use ueff to measure the $µ_{eff}$
Lab 3 Study of Inverter
This lab focus on the CMOS inverter, students are expected to and find the actual characteristics of the 45nm gpdk library for the concepts discussed in the lectrue. MDL script for lab 3 was provided as example. Since the SPECTRE script of the inverter had already provided in SPECTRE circuit script for lab 0, SPECTRE circuit script for lab 3 is a slightly modified version of lab0.
Measure $t_{pHL}$ and $t_{pLH}$
The $t_{pHL}$ and $t_{pLH}$ is defined as follows:
- $t_{pHL}$: delay from input 50% to outupt 50% when output is falling.
- $t_{pLH}$: delay from input 50% to outupt 50% when output is rising.
From the practice of this lab, we introduced two ways of delay measurements:
- One simple way is directly use the rising time and falling time at certain node as a surrogate measurement of the delay. Such a measrument will results in a difference compared to the actual measrument following the definition, while reflect the trend for such a simple circuit. It can be measured by using MDL below, included in the MDL script for lab 3.
// computation of risetime for signal V(out0) from 10% to 90% export real rise=risetime(sig=V(out0), initval=vdd*.1, finalval=vdd*.9) //computation of falltime for signal V(out0) from 90% to 10% export real fall=falltime(sig=V(out0), initval=vdd*.9, finalval=vdd*.1)
- The accurate method follow the definition of $t_{pHL}$ and $t_{pLH}$. It start the measurement when the input signal reach the threshold in certain direction, and stop it when the target output signal reaches predefined direction with certain threshold. Such a measurement resulting more accurate measurement while incurs extra difficulty when involves optimization. It can be measured by using MDL below, included in the MDL script for lab 3.
//computation of of actual tplh based on the definition export real tplh1 = deltax(sig1=V(in1), sig2=V(out10),dir1='fall, thresh1=vdd*.5,dir2='rise, thresh2=vdd*.5, start1=0, start2=0) //computation of of actual tphl based on the definition export real tphl1 = deltax(sig1=V(in1), sig2=V(out10),dir1='rise, thresh1=vdd*.5,dir2='fall, thresh2=vdd*.5, start1=0, start2=0)
Change the parameter
The reason to encourage highly parameterized design is to allow the simple measurements when we only want to change select parameter for some values. Below is the example need to included in the MDL script for lab 3 to power supply and run the transicent analysis.
foreach vdd from {0.5,0.6}
{
run rise_fall_trans
}
Lab assignements
Based on the provided example, students are expected to find and compute explore the CMOS inverter’s characteristics using 45nm gpdk library. Below are the ones we do in this semester:
- Construct a CMOS inverter with input port labeled as $V_{in}$, and both NMOS and PMOS set as W=300n, L=100n.
- Find the $t_{pHL}$ and $t_{pLH}$ in .measure file.
- Analyze the DC characteristic of the CMOS inverter:
- Set the Length of the NMOS and PMOS as a constant: 100n; Width of the NMOS as a constant: 300n.
- DC analysis the VIN (x axis) from 0 to 1.1v with a step of 0.01v
- Change the Beta ratio of the NMOS and PMOS by sweeping the Width of PMOS from 200n to 1000n with a step of 100n.
- View the VOUT (y axis) plot.
- Use the measurement tool and graph to find the closest PMOS width that has the Switching Threshold equal to $V_{dd}/2$. We use this balanced inverter for the following tasks. It can be identified within viva by click Marker->create marker->horizontal ->$V_{dd}/2$
- Set PMOS’s width be the value you found in previous bullentin, you need to find the delay ($T_p$) as a function of $V_{dd}$ by change the supply power supply from 0.5v to 1.1V with step of 0.1V. The results will shown in ‘.mt’ file. Remember, you need to measure both $t_{pHL}$ and $t_{pLH}$ in order to get the delay $T_p$. After you have found the inverter delay for each $V_{dd}$, you need to plot these data ($V_{dd}$ being X axis, and $T_p$ being Y axis) using any proper tool (e.g., excel, MATLAB).
- In this part, you need to find the device sizing versus delay $T_p$, here you need to measure $T_p$ with different size of CMOS inverter: 1:1:6 multiples of the width for both NMOS and PMOS in the balanced inverter. In this process, you need to connect the Inverter with different NMOS/PMOS width with TWO balanced inverters, find in the third bullentin. After that, you need to MDL commands. Then, use appropriate tool (e.g., excel, MATLAB) to plot the data (Width being X axis, and $T_p$ being Y axis).
Lab 4 Delay of combinational logic
This lab extend the study of inverter in previous lab, and explore CMOS combinational logics in 45nm library. The students are provided SPECTRE circuit script for lab 4 and MDL script for lab 4 using inverter as example for reference.
Capacitance connection
Capacitor named as C0 can be connected node net13 with value of CAP to the circuit using the below syntax
C0 (net13 0) capacitor c=CAP
Verifying combinational logic functionality using parameter set
For a $n$ input combinational logic, there is a possible $2^n$ input combinations. Also consider when we do the worst case delay analysis, we need to find the condition when only one single input’s voltage value was changed. Thus, we need to explore a new syntax in SPECTRE, name paramet to enumerate all possible initial and terminal value combinations. If initial value is identical to terminal value, then there is no change. It facilitates the worst-case delay analysis. Also, by changing the period of the individual input ports’ pulse wave, we can examine the functionality of the combinational logic with full coverage. Below is the example file avaliable in SPECTRE circuit script for lab 4
v1 (in0 0) vsource dc=vs type=pulse val0=init_a val1=term_a period=10u rise=5p fall=5p width=5u
init_val paramset{
init_a term_a init_b term_b
0 0 0 0
0 0 0 vdd
}
MDL Optimization syntax
The MDL optimization follows the script below in high level structure, with more detials avaliable in MDL_workshop_tut.pdf under the installation path. By changing the zero statement as optimization objective and changing the parameter needs to optimize, the SPECTRE tool will try its best to find the parameter fits the optimization goal.
mvarsearch_statement ::=
mvarsearch {
option {options_statements}
parameter {parameter_statements}
exec {exec_statements}
zero {zero_statements}
}
Lab assignements
Based on the provided example, students are expected to find and compute explore the CMOS inverter’s characteristics using 45nm gpdk library. Below are the ones we do in this semester.
- Build an inverter as the first stage of your inverter chain (NMOS: 300n/100n; PMOS: 600n/100n. Connect 64 identical inverter at the end of inverter chain to serve as the load capacitance.
- Construct four inverter chains for $N$ (number of stages) from 1 to 4. For the rest of the stages, you need to set the CMOS parameters for inverters (except the first one) based on the total number of stages and the design rule learned in class.
- Measure the Delay ($T_p$) for each inverter chain (final output), and here you still need to measure both $t_{pHL}$ and $t_{pLH}$ in order to get the delay $T_p$.
- Construct a CMOS inverter, make the width (300n) and length (100n) fixed for NMOS, and length (100n) fixed for PMOS. Using the MDL Optimization tool, find the width of the PMOS for each of the following requirements:
- Make $t_{pLH}-t_{pHL}$ as close to zero as possible
- Have the smallest average propagation delay (hint: make $(t_{pLH}+t_{pHL})/2$ as close to zero as possible)
- Use the MDL Optimization tool to find the width of the PMOS that makes the switching threshold ($V_m$) equals to half of $V_{dd}$. Note that this is a DC analysis.
- CMOS combinational gate design:
- Build the 2-input NAND gate, and 2-input NOR gate. Keep the NMOS/PMOS of this gate length at 100nm, and NMOS width with 300nm and PMOS width with 600nm. Since here, we only care about functionality.
- Verify the functionality by feeding in the pulse wave for all possible input combinations. Take a screenshot of it.
- The Logical effort is the ratio of a gate’s input capacitance to an inverter’s input capacitance, delivering the same output current. As mentioned in the slide, it can be measured from delay vs fanout plots.
- Build an inverter with an NMOS/PMOS length with 100nm, and NMOS width with 300nm and a PMOS width that satisfies the non-skewed inverter derived in problem 2.
- Use the 2-input NAND gates and 2-input NOR gates built previously, and size it that can deliver identical output current as the inverter built in previous bullentin. Note that it is possible to use an optimization tool to find the more realistic width using an optimization tool, which is not required here.
- Find the worst case propagation delay for inverter, 2-input NAND gate, and 2-input NOR gate when their load is 1, 2, 3, 4 copy of itself. Find the slope of the delay, then report the founded logical effort and verify the concept.
- Verify the worst-case propagation delay input patterns by MDL for the 2-input NAND gate and 2-input NOR gate.
- Build the 3-input NAND gate and 3-input NOR gate, and size it properly according to the inverter built in a, according to the slide.
- Find the worst-case propagation delay for gates when load is 1,2,3,4 copies of itself. Find the slope of the delay trend, then report the founded logical effort and verify the concept.
- Verify the worst-case propagation delay input pattern as shown in the lecture using MDL for the 3-input NAND gate and 3-input NOR gate.
- Using the 2-input, 3-input NAND gates derived in the previous step. Perform progressive sizing of NMOS to examine the difference between different propagation delays. Suppose the topmost NMOS gate size derived in the previous step is W_nmos:
- For 2-input, the NMOS size from top down become W_nmos, W_nmos/2.
- For 3-input, the NMOS size from top down become W_nmos, 3*W_nmos/4, W_nmos/2.
- Examine the change of worst-case delay in this case and discuss why it happened?
- Using mdl optimization tool to find the smallest worst-case delay for 2-input and 3-input NAND gate by only changing the bottom 1/2 NMOS gate, does that fit your expectations?
Lab 5 Combinational Logic Family, Wire, Sequential Logic
This lab serves as the last regular lab for this course. Here, the students are expected to examine the remaining concepts that haven’t verified in the previous labs. No custom example script is provided for this lab since students are expected to have fimilarized with the SPECTRE design.
A select subset of new commands are used in this lab:
Resistor connection
Similar to the capcitor connection, resistor can be connected to the circuit as shown below by identifying the name of the resistor, the two ends of resistor connections and its value.
R0 (net10 0) resistor r=10
Point-wise signal definition
The point-wise signal can be defined as follows, with the format of time and desired voltage at that time.
vdata (d 0) vsource type=pwl wave=[0 0 0 0 1n vdd 10n vdd 11n 0]
Lab assignements
- Verify the Elmore delay in SPECTRE. Connect the resistors and capacitors as shown in the circuit diagram below, where R=100Ohm and C=100pF.
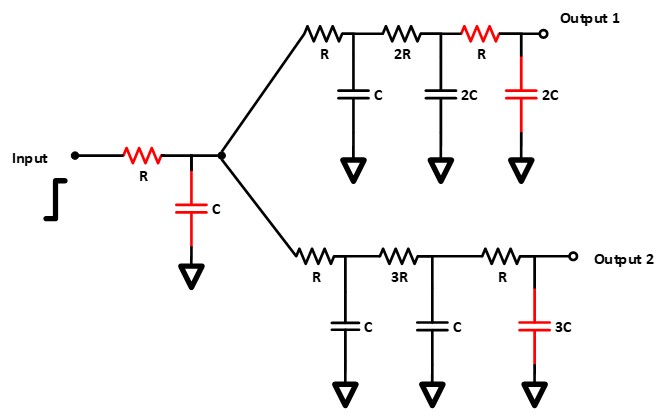
- Measure the Propagation delay of the circuit diagram from the input and output1 and output2. Measure the time from the start of the input rise to the 50% of output rise.
- Compute the Elmore delay.
- Convert the Elmore delay to the propagation delay (multiply Elmore delay by 0.69) .
- Compare the difference by measuring the percentage by (Propagation delay in a measured by SPECTRE- Propagation delay in previous bullentin)/(Propagation delay in a measured by SPECTRE).
- Change the length of wire to 0.5, and 2.0 unit of original wire length, redo previous three bullentins. Note that the Resistor and Capacitor in red are NOT WIRES. Please notice the changing pattern of resistance and capacitance of the length. $R=R_\square \frac{L}{w}, C=\frac{\epsilon S}{4\pi kd}$
- [NOT REQUIRED] Using the above Resistor-Capacitor connection, how can we minimize the delay by changing the length of the wire for two paths individually using MDL optimization tool or computed analytically?
- Design the 2 to 1 MUX using the transmission gate and CMOS.
- Verify the functionality for both designs.
- Compare the output waveform’s voltage of the transmission gate and CMOS gate implementation, find any differences between them.
- Measure the delay for all input-output patterns for both design, and find the worst case of them.
- Design a CMOS logic, unfooted Dynamic logic, footed Dynamic logic for the following: $Y=A’B+AC$
- Verify the functionality of built logic. You are free to introduce the variable’s complement if needed.
- For CMOS logic, check the functionality.
- For unfooted and footed dynamic logic, please make the $\phi$ with the smallest switching period to better observe the pre-charge->evaluate cycle. Start the $\phi$ with $0$.
- Compare the delay for all logic designs for all possible input combinations.
- Identify the monotonicity of the dynamic logic.
- Change the $\phi$ to a larger period and observe the charge leakage process, take a screenshot the waveform.
- Change the $\phi$ to an even larger period, making the output logic cannot recover until it reaches another pre-charge cycle, take a screenshot the waveform.
- Verify the functionality of built logic. You are free to introduce the variable’s complement if needed.
- Fix all widths and lengths of PMOS and NMOS, with PMOS width=600nm, NMOS width=300nm, and length=100nm. The SPECTRE code for D-flip flop is the exact copy avaliable under the MDL workshop directory. Keep the clock period at 80ns, and find a single D-flip flop’s setup time and hold time. To find the setup time and hold time, you need to draft your MDL file by measuring the delay from clock rising edge to the Q’s rising edge, both at 0.5*vdd. Then, you need to change the point-wise signal’s rising time and falling time to find the setup time and hold time per definition.
Unused lab assignements
- Ring oscillator
- Please build the 5-stage ring oscillator using inverter with NMOS/PMOS length of 100nm, NMOS width of 300nm, PMOS width of 600nm. You may use a subcircuit to facilitate the building process.
- Please measure the oscillation frequency of such a circuit.
- Use the Monte Carlo method discussed during the previous lab session. Try to have multiple sets of PMOS/NMOS sizing with different parameters under identical distribution, what’s your finding? What could be the possible use case for such a design?
- Multi-output combination circuit simulation verification.
- Verify the worst case delay combination.
- Verify the delay of branching. Load two branch outputs with identical capacitance load.
- Try to change the capacitance load of the branch with a larger worst case delay , and try to make two branches worst cast delay, Is such a change identical to the theoretical analysis?
- NMOS and PMOS transmission gate.
- Build the circuit diagrams as the ones in Question 2.20 for CMOS VLSI Design: A Circuits and Systems Perspective, and verify if the simulation result fits the analytical one.
- Exchange the source and drain of the connection, is that fit your expectation?
Lab 6 Final project 2-bit full adder
In this semester’s final project, the topic is 2-bit full adder. The project requires the students first to design the CMOS 2-bit full adder by themselves. Then the design is expected to minimize the total number of transistors by bubble pushing. After that, optimization tool is used to minimize the worst case delay in the designed circuit iteratively.
The requirements are listed below:
- Design is required to using available 45nm gpdk in Cadence.
- Trying to implement the entire logic using 2-input NAND gate or NOR gate built by CMOS. Inverters are only allowed at the input buffer stage.
- Trying to minimize the delay for worst case possbile input combinations. The one who received minimal delay gate size prodcut receive extra credits.
- Try to minimize the area (measured by width) and worst-case delay (measured in ns) product as typical IC design targets, the lower the product, the better the performance.
Lab Extra RTL2GDSII workflow
In prior offerings, students also given the expierence of sythesizing the digtial circuit written in Verilog, extract the sythesized netlist, and examine the timing performance and
In this semester, part of the workflow was introduced, and complete workflow for cadence 45nm library is updated below.
Cadence example workflow download
The example RTL2GDSII workflow is available under the Cadence training portal named as Cadence RTL-to-GDSII Flow Training.
Verilog compliation and simulation
Verilog sythesis
Verilog implementation
EDA algorithm under the hood
Though it is not required to understand the underlying mechanisim of teh RTL2GDSII workflow,Verilog implementation, students are encouraged to watch the following MOOC course to have a deepen understanding about the EDA algorithm, named as VLSI CAD Part I: Logic, VLSI CAD Part II: Layout.
